Authors:
(1) Nhat A. Nghiem, Department of Physics and Astronomy, State University of New York (email: nhatanh.nghiemvu@stonybrook.edu);
(2) Tzu-Chieh Wei, Department of Physics and Astronomy, State University of New York and C. N. Yang Institute for Theoretical Physics, State University of New York.
Table of Links
Acknowledgements, Declarations, Data Availability Statement, and References
Following the celebrated quantum algorithm for solving linear equations (so-called HHL algorithm), Childs, Kothari and Somma [SIAM Journal on Computing, 46: 1920, (2017)] provided an approach to solve a linear system of equations with exponentially improved dependence on precision. In this note, we aim to complement such a result for applying a matrix to some quantum state, based upon their Chebyshev polynomial approach. A few examples that motivate this application are included and we further discuss an application of this improved matrix application algorithm explicitly with an efficient quantum procedure.
I. MAIN PROCEDURE

The error dependence O(1/ϵ) is a result of the quantum phase estimation (QPE) subroutine used in HHL algorithm. This dependence has been significantly improved in [2] to scale as O(poly(log(1/ϵ))). As mentioned in [2], due to the finite-bit precision required to achieve an error ϵ eventually, the QPE subroutine in [1] limits a better scaling of error dependence. Instead, the authors of [2] outlined two approaches based on Fourier and Chebyshev series decomposition. These two methods are implemented differently, but they share the same striking property: their truncations at relatively low orders (∼ O(poly(log(1/ϵ))) guarantee an approximation error ϵ of the given function, i.e., 1/x, for the matrix inversion. These series decompositions are then integrated into quantum algorithms thanks to a procedure to apply a linear combination of unitary operators. Details can be found in [2], and, in particular, see their Lemma 6 and Lemma 7.

As worked out in [4], multiplication of a matrix is an adaptive version of HHL algorithm [1]. After the QPE step, one simply performs controlled-rotation on the ancilla with the multiplied eigenvalues (instead of dividing them) to achieve the goal of multiplication (see [1, 4] for details). Since it is just a slight modification of the HHL algorithm, the QPE subroutine is still employed and hence, the running time still scales as O(1/ϵ). It is very natural to ask if such an error scaling could be improved to O(poly(log(1/ϵ))), as for the matrix inversion case. The answer is affirmative, and it is surprisingly simple to achieve this, as we explain below.
We now discuss the Chebyshev series approach in [2]. The two main ingredients of this approach are: (1) approximating a function (in the matrix inversion case, it is 1/x) by a linear combination of Chebyshev polynomials, and (2) implementing each Chebyshev polynomial by a quantum walk [6]. In [2], all these ingredients are discussed comprehensively, and hence we would not repeat the details here. Instead, we recapitulate a key result from there. For completeness, a brief review of key ingredients from [2] is provided in Appendix A.





Before we head into some applications, we make a quick comparison between our improved matrix multiplication algorithm versus previously known method for multiplying matrix, which occurs in the context of data fitting [4]. For completeness, the statement of the matrix multiplication problem is, for a given state |b⟩, we need to prepare the state A |b⟩ /|A |b⟩ | where |.| refers to the norm. In their work [4], the authors essentially adapt HHL algorithm [1] to implement matrix multiplication by simply adjusting the phase rotation step, which produces the desired state in time
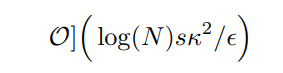
Meanwhile, as we pointed out in Thm 1, the desired state could be produced in time that scales polylogarithmically to most of parameters, except sparsity s. It demonstrates the quite surprising power of the Chebyshev approach that was first employed in [2]. Furthermore, in this approach, only a single query to entries of A is being used.
This paper is available on arxiv under CC 4.0 license.

