Authors:
(1) Anatol Guglielmi, Schmidt Institute of Physics of the Earth, Russian Academy of Sciences;
(2) Boris Klain, Borok Geophysical Observatory of Schmidt Institute of Physics of the Earth, Russian Academy of Sciences;
(3) Alexey Zavyalov, Schmidt Institute of Physics of the Earth, Russian Academy of Sciences;
(4) Oleg Zotov, Schmidt Institute of Physics of the Earth, Russian Academy of Sciences and Borok Geophysical Observatory of Schmidt Institute of Physics of the Earth, Russian Academy of Sciences.
Table of Links
Omori (1894)
It is best to start describing the outstanding events of a century ago from afar. In 1850, John Milne was born in Liverpool, who in the future was to become a famous geophysicist, one of the founders of modern seismology [15]. He was educated in London, worked as a mining engineer in Newfoundland, as a geologist in the Sinai Peninsula, and from 1875 to 1895 worked in Tokyo at the invitation of the government of the Japanese Empire. It is curious that in search of adventure, Milne traveled to Tokyo for three months, mostly by land (via Siberia). In 1880, he created a horizontal pendulum seismograph - the first easy-to-use and sufficiently sensitive instrument for recording earthquakes.
In 1887 Milne was elected a member of the Royal Society. He manages to convince the Society to allocate funds for the creation of a world network of seismic stations equipped with his instruments. Japan highly appreciated Milne's services to the country and the world. Emperor Meiji awarded him the Order of the Rising Sun and awarded him a lifetime pension of 1,000 yen. The University of Tokyo elected him honorary professor.
Fusakichi Omori was a student of John Milne. He enjoyed the encouraging support of his teacher, as did all young Japanese seismologists of that time. On October 28, 1891, the earthquake with a magnitude of M = 8 occurred. Milne's seismographs recorded numerous aftershocks. Analysis of these aftershocks allowed Omori to formulate the law that bears his name [2]. It is worth mentioning that he was 26 years old at the time.
Omori's Law states that after a strong earthquake, the frequency of aftershocks, i.e. tremors following the main shock, on average, decreases hyperbolically over time:

Here k > 0, c > 0, t ≥ 0. This was the first law of earthquake physics, if we keep in mind the chronological sequence of outstanding discoveries in seismology.
Intuition tells us that the Omori formula (6) has the characteristics of a fundamental law of nature. Let's explain what was said. Firstly, (6) can be rewritten in the equivalent form n kt = /, where k > 0, t > 0. In fact, contrary to popular belief, the parameter in (6) is free due to the homogeneity of the flow of time t. In other words, Omori’s law is one-parameter: the value of k generally characterizes the source of an earthquake over the entire history of the evolution of aftershocks.

The general solution of equation (2) is

Taking (1) into account, it is easy to see that Omori’s law (6) follows from (7) under the condition s = const . In this case k =1/σ , 0 c n =1/ σ . In other words, Omori's law is satisfied provided that the deactivation coefficient remains unchanged throughout the entire history of aftershock excitation.
The found condition for the applicability of the Omori law is tough. Is it carried out experimentally? To answer the question, we compiled the Aftershock Atlas [8], which presents solutions to the inverse source problem. The characteristic size of the source was determined according to the method [16].
Analysis of solutions for several dozen events indicates that in all cases, at the first stage of the evolution of aftershocks, immediately after the main shock, the source deactivation coefficient remains unchanged within the limits of measurement accuracy. We call the time interval during which s = const the Epoch of Hyperbolic Evolution (EHE) , or Omori epoch. The duration of EHE varies from case to case from a few days to several months. Figure 1 shows a case of a fairly long EHE, almost equal to 100 days. There is a tendency for σ to decrease with increasing magnitude of the main shock [17].
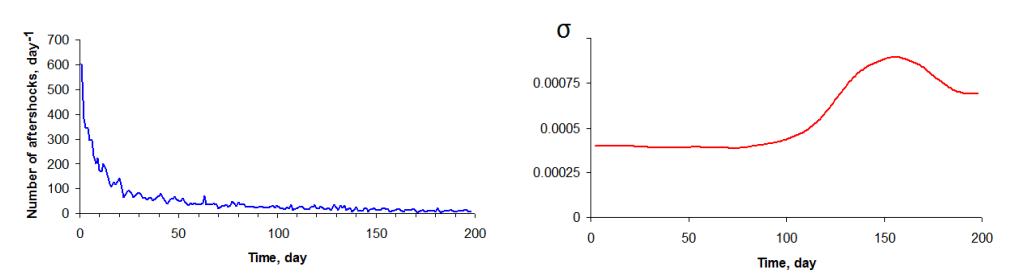
The discovery of the Omori epoch is extremely significant. At the end of the epoch, the state of the source changes. Let's introduce parameter θ = dσ / dt. In the Omori epoch, θ = 0. The transition to a new state is indicated by a sharp jump in parameter θ (Figure 2). This suggests that the end of the Omori epoch is accompanied by a bifurcation of the earthquake source.
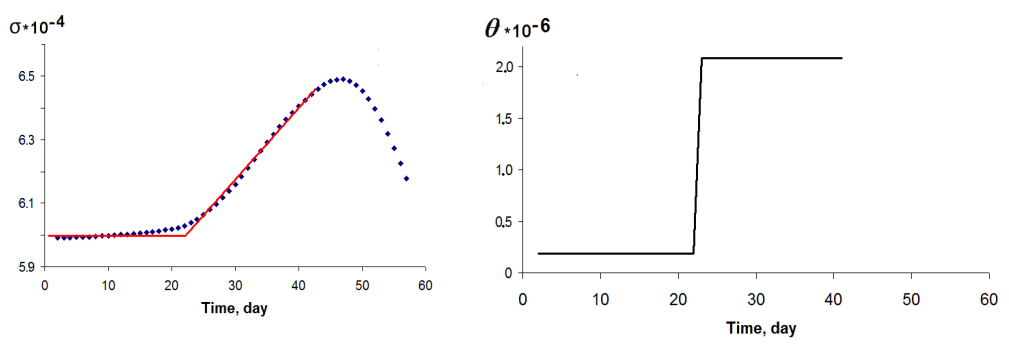
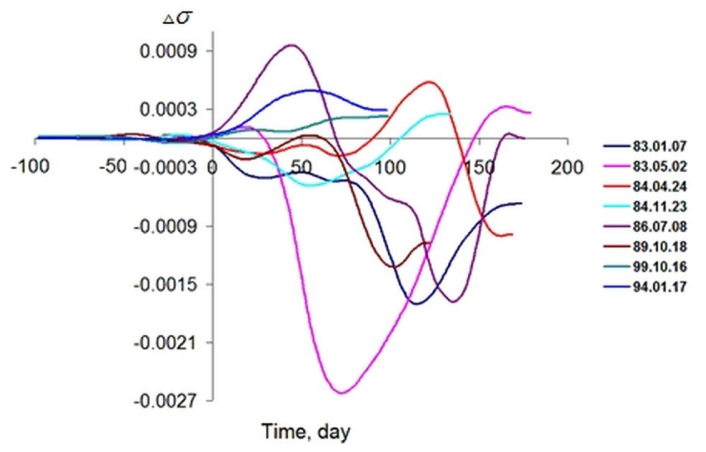
A convincing illustration of this is Figure 3. It shows the result of processing and analyzing eight events. The transition from one mode of source deactivation to a qualitatively different mode is abrupt in the sense that its duration is much less than the duration of the Omori epoch.
Let us summarize the preliminary results of studying the evolution of aftershocks by solving the inverse problem:
- 1The Omori formula (6) has the status of a law that is fulfilled with good accuracy in a real geophysical process.
-
The applicability of Omori's law is strictly limited to the epoch of harmonic evolution of the earthquake source.
-
At the end of epoch of harmonic evolution, the source experiences a bifurcation.
To conclude the section devoted to Fusakichi Omori, let us return to formulas (6) and (7).
The law of aftershocks (7) formally differs from law (6) only in that in it time t is replaced by proper time τ . The concept of proper time and the corresponding term were introduced into physics only at the beginning of the 20th century. It would seem that Omori simply did not have the opportunity to use the concept of proper time in order to give formula (6) the flexibility and physical meaning that our formula (7) has. In this regard, we want to clarify that the source proper time (1) is not directly related to the relativistic proper time. Formulas of the form (1) express the uneven functioning of any dynamic system immersed in a nonstationary environment or located in nonstationary external force fields. In our case, formula (1) takes into account the non-stationary state of the source that experienced the main shock of the earthquake.
This paper is available on arxiv under CC BY 4.0 DEED license.

